The problem is: find the number of all different monolinear curves (i.e. the corresponding mirror arrangements) which could be derived from a rectangular grid RG[a,b] with the sides a, b, covered by k curves, for a given number of mirrors m (m = k-1, k, ..., 2ab-a-b).
Unfortunately, we are very far from the general solution of this problem. Reason for this is: every introduction of an internal mirror changes the whole structure, so it behaves like some kind of "Game of Life" or cellular automata, where a local change results in the global change.
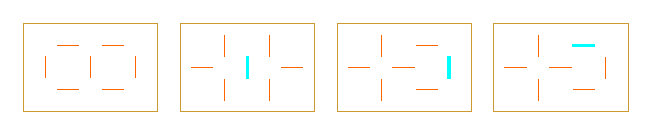
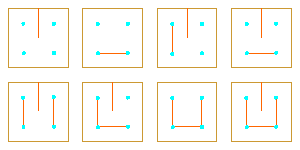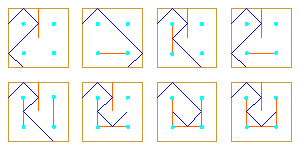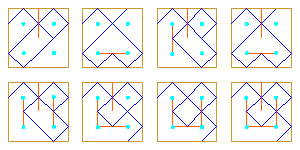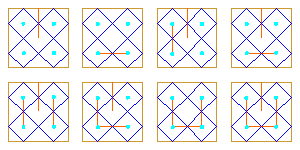
For example, if the possible positions for an additional internal mirror are orange, after introducing it (turquoise mirror), the possible positions for the next (orange) mirror depend from its position.

Till now we have only few combinatorial results, obtained
for some particular cases by S.V.Jablan, and
generalized by G.Baron. Let be given a rectangular grid
RG[a,b], k = gcd(a,b) (gcd - greatest
common divisor), and let be
introduced the minimal number k-1 of two-sided internal mirrors
incident to the cell-edges. If
t = (ab-lcm(a,b)):(k(k-1)) = 4xy
(lcm - lowest common measure),
x = a:(2k), y = b:(2k), we have
the following results, where for different k are given the
conditions for a, b, and the number of curves:
with k-1 only edge-incident mirrors, and a nonequal to b,
for k odd
Even for some smaller rectangles (e.g. a = 6, b = 3), and minimal number of mirrors (k-1 = 2), the number of the different curves obtained is large enough. G.Baron also derived formulas for the case a = b with the larger groups of symmetries and, finaly, constructed for k = a = b equal 2 or 3 and the maximum number of mirrors all different mirror-schemes. There is only one for k =2 and 28 for k=3.
For example, there are 52 different arrangements of two edge-incident mirrors in a rectangle 6x3 producing perfect curves. Among them, only 8 are symmetrical - 4 mirror-symmetrical and 4 point-symmetrical.
