|
3. Knot theory and fullerenes Let be given an oriented knot or link diagram D with generators g1,…, gn [12]. If the generators gi, gj, gk are related as in Fig. 6a, then aii= -t, aij= 1, aik= -1; if they are related as in Fig. 6b, then aii= t, aij= 1, aik= -1; in all the other cases aij=0. The determinant d(t)=|aij| is the polynomial invariant of D. In the case of links, in this polynomial invariant we use for generators of different components different variables (up to a permutation of variables). For example, let us show that two isomers of C20 are different (Fig. 3-4, 6c). After converting their chemical Schlegel diagrams into the alternating knot diagrams, denoting their generators, and calculating the corresponding determinants we obtain, respectively, D1=t20 -10t18+45t16-120t14 +200t12-197 t10 +105t8-40t6+25t4 -10t2 and D2=t20 -10t18+45t16-120t14 +208t12-250t10 +217t8-130t6+49t4 -10t2, proving their difference. On the other hand, for three-component alternating links corresponding to the diagrams (Fig. 6d), using the same multivariable invariant for link projections, we conclude that they both represent the isomorphic Schlegel diagrams of the same fullerene C24. 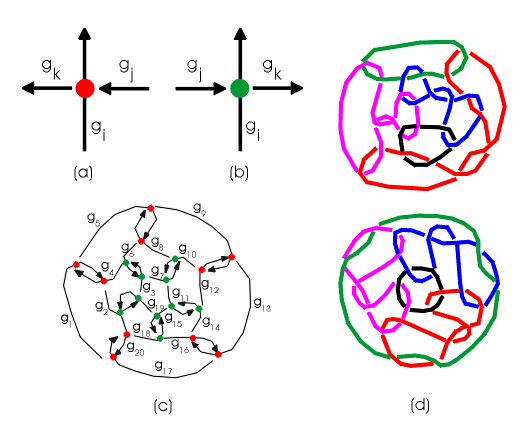 |