Here is the problem by Louis Carrol: make a contur drawing of this figure by a singular closed line, never passing twice through the same point. Find all solutions! The first question is: is there any solution? The answer is - yes, because the contur is an Eulerian graph: in every vertex there is an even number of edges. Try to prove this general statement! How many different solutions exist if the curve may have a finite number of self-intersection points?
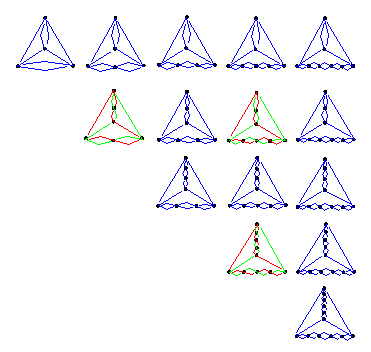
Every Eulerian graph is a projection of some knot or link and vice versa Such a projection is called regular if the graph is 4-regular, i.e. if the valence of every vertex is 4. Otherwise, the projection is irregular. By slightly changing it, it is always possible to turn some irregular projection of a knot or link into a regular one. Two knot or link projections are isomorphic (or simply, equal or same) if they are isomorphic as the graphs on a sphere. Trying to find all nonisomorphic projections of alternating knots and links with n crossings, we need to find all nonisomorphic 4-regular planar graphs with n vertices and vice versa Among them, we could distinguish graphs with or without digons. If we denote digons by colored edges, we could imagine the trefoil as a triangle with all colored edges, the knot 41 as a tetrahedron with two colored nonadjacent edges, Borromean rings as an octahedron...

After that, you could replace every digon by a chain of digons, and obtain different families of knots and links. For example, this is the family generated by the knot 41 If you like that "geometrical" way of thinking about knots and links, see the paper "Geometry of links" by S.V.Jablan.