|
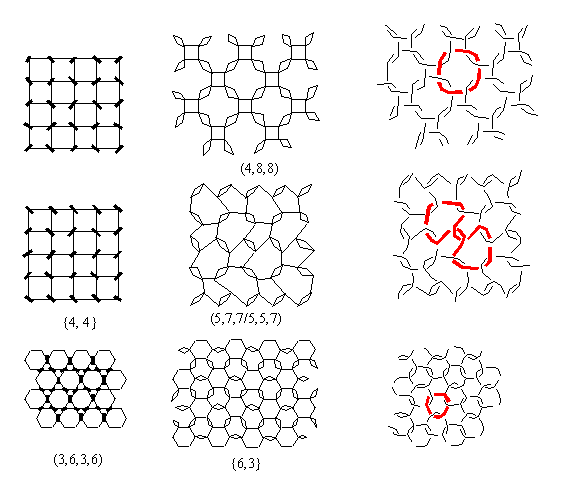
6. Fullerenes on other surfaces Different regular homoatomic C plane nets are discussed by
T.Balaban [18]. They could be derived
in the same way as the general fullerenes: by introducing digons in the
vertices of 4-regular graphs or by an edge-coloring of a 3-regular graph,
resulting in 4-regular one. For example, we could start from the regular
tessellation {4,4}, Archimedean tiling (3,6,3,6) or 2-uniform tiling (3,42,6;3,6,3,6)
that all are 4-regular [19], and
introduce digons in their vertices, or from regular tiling {6,3} that is
3-regular and color its edges (Fig.
18). From 3-regular tilings we could also derive "perfect" plane nets
in the same way as before.
 For different surfaces, the necessary condition for general
fullerenes follows from Euler theorem v-e+f=2-2g,
where g is the genus of the surface. For the torus g=1, so
accepting 5/6 restriction we conclude that for 3-regular graphs n5=
0. In this case, the only possibility is the regular tessellation {6,3},
consisting of b2+bc+c2 hexagons
(where b,c are natural numbers) [5].
This tessellation we could obtain identifying opposite sides of the rectangle
(Fig. 19).
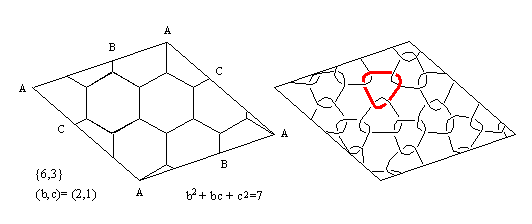 From such finite {6,3} we could simply derive the corresponding
"perfect" hexagonal fullerene on torus. The proposed approach could be
extended also to the double, triple, etc. torus with g=2,3,… Similar
transformations of C nets from one surface to the other (e.g. from plane
to cylinder, and then to torus) maybe could explain the formation of certain
fullerenes and their growing process [20].
 Accepting that the faces could be also heptagons or octagons,
from the relationship 2e=3v and Euler formula, follows that
n5-n7-2n8= 12(1-g).
For a sphere without octagons, n5-n7=12,
and for a torus without octagons n5=n7
[21]. To obtain such general fullerenes
with a higher degree of symmetry, we could start from different vertex-transitive
structures (e.g. uniform polyhedra, stellated regular and semi-regular
polyhedra or infinite polyhedra) [21].
For example, different uniform 4-valent polyhedra of the type (3,q,3,q)
(q=7,8,9,10,12,18) could be used for the derivation of the corresponding
"perfect" fullerenes with q-gonal holes on a double torus (g=2)
(Fig. 20, q=8 [22]).
For this, we use the regular vertex-bifurcation of triangular faces, transforming
all of them into hexagons. In the same way, the uniform tessellations of
the type (4,q,4,q) (q=5,6,8,12) or (5,10,5,10) of
a double torus may result in different finite general fullerenes. The interesting
classes of infinite general fullerenes with non-euclidean plane symmetry
groups could be derived from the tessellations of hyperbolic plane H2.
For example, from the uniform tessellation (3,7,3,7) we derive the infinite
perfect 6/7 fullerene in H2 with heptagonal holes (Fig.
21)[21]).
 |